 Indexing
Indexing
 All Issues
All Issues
 Submission
Submission
 Author Guidelines
Author Guidelines
 Reviewers
Reviewers
 Editorial Members
Editorial Members
 Publication Fee
Publication Fee
Vol.3 , No. 1, Publication Date: Mar. 2, 2016, Page: 19-25
| [1] | Faith U. Babalola, Department of Chemical and Petroleum Engineering, University of Lagos, Akoka-Yaba, Lagos, Nigeria. |
| [2] | Oluwatosin S. Famoroti, Department of Chemical and Petroleum Engineering, University of Lagos, Akoka-Yaba, Lagos, Nigeria. |
The Thermodynamic Modeling Framework (TMF) for LNG systems is obviously not available and its focal point is the development of robust methods for thermodynamic stability analysis as well as algorithms for accurate phase split predictions. A new model is here developed with its algorithm and applied to a Nitrogen-rich LNG system. Two EOS models were used with initial 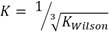 With Peng-Robinson EOS model, 2-phase split occurred at 110.8K, 3-phase–split occurred at 110.9K while the system reverted to 2 phases at 111K without further changes. For the Soave-Redlich-Kwong EOS model, the system split into 2 phases at110.8K, into 3 phases at 11K but reverted and remained a 2-phase system at 111.8K.
With Peng-Robinson EOS model, 2-phase split occurred at 110.8K, 3-phase–split occurred at 110.9K while the system reverted to 2 phases at 111K without further changes. For the Soave-Redlich-Kwong EOS model, the system split into 2 phases at110.8K, into 3 phases at 11K but reverted and remained a 2-phase system at 111.8K.
Keywords
LNG, TMF, Phase Stability, Phase Split
Reference
| [01] | Blanca E. Garcia-Flores, Justo-Sarcia D. N., Stateva R. P., Garcia-Sanchez F. (2012) Phase Behaviour Prediction and Modelling of LNG Systems with Eoss- What is Easy and What is Difficult? Advances in Natural Gas Technology. ROUMIANA PETROVA STATEVA, vol. 14: 359-363. |
| [02] | Adewumi A. (2014). PNG 520, Phase Relations in Reservoir Engineering- Phase Behaviour of Natural Gas. The College of Earth and Mineral Resources. The Pennsylvania State University, www.e-education.psu.edu/png520. |
| [03] | Ayala, L. (2006). Phase Behaviour of Hydrocarbon Fluids –The Key to Understanding Oil and Gas Engineering Petroleum and Natural Gas Engineering, the Pennsylvania State University. Business Briefing: Oil & Gas Proc. Review. 2006: 18. |
| [04] | Dashtizadeh G., Pazuki G. R., Taghikhani V. and Ghotbi C. (2006) A New Cubic Equation of State for Predicting Phase Behavior of Hydrocarbons. Oil and Gas Science and Technology –Rev. IFP, Vol. 61, No. 2, 269-276. |
| [05] | Firoozabadi A., SPE, and Pan H., SPE, (2002). Fast and Robust Algorithm for Compositional Modelling. Reservoir Engineering Research Institution, Part 1 - Stability Analysis Testing SPE Journal Vol. 7: 78, 79. |
| [06] | Haugen K. B., Firoozabadi A, Kjetil B., Sun L. (2011). Efficient and Robust Three-Phase Split Computations. Chemical Engineering Dept., Mason Laboratory, Yale University, Reservoir Engineering Research Institute (RERI), 12452 Aiche Journal Vol. 57, No 9: 2555-2557. |
| [07] | Naji H. S. (2008). Conventional and Rapid Flash Calculations for the Soave-Redlich-Kwong and Peng-Robinson Equations of State. King Abdulaziz University, Jeddah, Saudi Arabia. Emirates Journal for Engineering Research, 13 (3): 81-85. |
| [08] | Rosales-Quintero A. (2009) Isothermal Flash Calculation Using Soave Equation of State Multicomponent Flash Calculations Using an Equation of State and Classical Mixing Rules. File ID: #22364, Version: 1.1 MATLAB CENTRAL 1994-2013 The Mathworks, Inc. |
| [09] | Iranshahr A., Voskov D., Tchelepi H. A. (2010). Generalized Negative-Flash Method for Multiphase Multicomponent Systems Department of Energy Resources Engineering, School of Earth Sciences, Stanford University, Elsevier B. V. Vol. 299, Issue 2: 272-274. |
| [10] | Michelson, M. L. (1982a). The isothermal flash problem. Part I. Fluid Phase Equilibrium. 9 (1): 1-19. |
| [11] | Baker, L. E. Pierce, A. C. and Luks, K. D (1982) Gibbs Energy Analysis of Phase Equilibria. SPE J 22 (5): 731-742. SPE-9806-PA. |
| [12] | Michelson, M. L. (1982b). The isothermal flash problem. Part II. Phase split calculation. Fluid Phase Equilibrium. 9 (1): 21-40. |
| [13] | Haugen, K. B. Firoozabadi, A. and Sun, L. (2011). Efficient and robust three-phase split computations. AIChE J. 57(9): 2555-2565. |
| [14] | Rachford, Jr, H. H. and Rice, J. D (1952). Procedure For Use Of Electronic Digital Computers In Calculating Flash Vapourization Hydrocarbon Equilibrium. Transactions of The American Institute of Mining and Metallurgical Engineers. Vol. 195. SPE 952327-G, 327-328. |
| [15] | Zhidong Li, Abbas Firoozabadi (2012a) Initialization of phase fractions in Rachford–Rice equations for robust and efficient three-phase split calculation Reservoir Engineering Research Institute (RERI). Fluid Phase Equilibria 332 (2012) 21–27. |
| [16] | Soave, G. (1972). Equilibrium constants from a modified Redlich-Kwong equation of state, Chem. Eng. Sci. 27: 1197- 1203. |
| [17] | Peng, D. Y. and Robinson, D. B. (1976). A New Two-Constant Equation of State. Industrial and Engineering Chemistry Fundamentals (15): 59-64. |
| [18] | Wilson, G. M. (1968). A Modified Redlkich-Kwong Equation of State, Application to General Physical Data Calculations. Presented at the 65th national AIChE meeting, Cleveland, Ohio, USA, 4-7 May, paper 15-C. |
| [19] | Zhidong, L. and Firoozabadi, A.:(2012b) General Strategy for Stability Testing and Phase Split Calculations in Two and Three Phases. SPE, RERI and Yale University. SPE journal December 2012: 1-6. |
| [20] | Introduction to LNG, Centre for Energy Economics. Liquid methane fuel characterization and safety assessment report. Cryogenic fuel Inc. CFI 1600, Dec. 1993: 17-20. |





